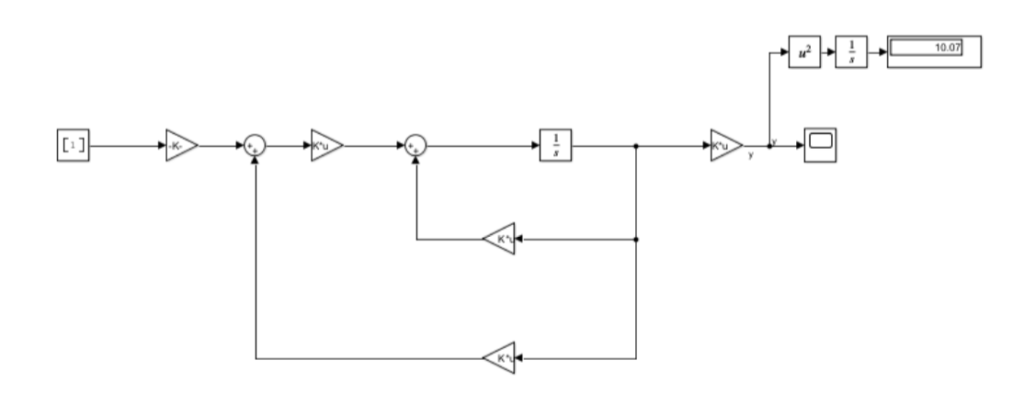
The closed loop system in Simulink, including feedforward gain and a measure for integral square error
The Project
One of the major deliverables for ENGR 480 – Modern Control, was to work in a group of 3 and find a model for a system. From this model, the group was to design a state-feedback controller (otherwise referred to as pole placement or full state feedback) and place the system’s poles at various locations, in other words, controlling the system.
For my group, we decided to use a model of a simplified vehicle break suspension system, which resulted in an A matrix of only 4×4, minimizing the difficulty in handling the system while also being complex enough to apply course concepts.
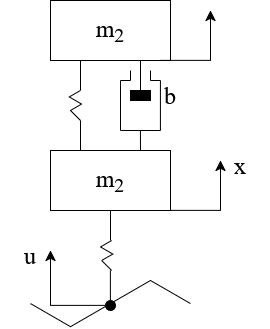
A visual representation of the vehicle suspension system used in the project
Design Process and My Contributions
The design project was split into several deliverables. The first deliverable involved actually finding the system to use. This was one of my major contributions to the team, as I was the one that found our system within the textbook of Modern Control Engineering by Ogata.
Once we had the system, we converted the system from its transfer function representation to its state space representation. From this, we found the system eigenvalues and its Jordan form representation.
Once we had the system dynamics, we could start playing with it. To begin, we looked at the responses the system had to various inputs, including a step response (pictured to the right), an impulse response, and a ramp response. From here, we looked at the system under zero input, zero state, and nonzero input and nonzero state conditions. Unfortunately (or fortunately) for us, the system provided to us was extremely well-behaved, being stable, observable, and controllable without any additional tinkering.
The project was fortunately a team effort from start to finish, with me and the other two members equally taking on the work, troubleshooting any errors with each other and maintaining constant communication.

Open-loop response of the system to a step input
Final Result and Conclusion
Our instructor for this course emphasized how powerful state feedback control is and the results speak for themselves. While our project was inherently “boring” in that everything worked out of the box, we were able to freely manipulate the system’s eigenvalues to produce a superior closed loop response.


Open-loop response of the system (left) and controlled closed loop response of the system designed to minimize settling time (right)
From the above pictures, it is clear how powerful pole placement is. Just by specifying where we want the system eigenvalues to be, we can design a gain that changes the input of the system to modify the A matrix to have such characteristics (provided the eigenvalues are controllable!)
One point of note is that while we managed to reduce settling time, it comes at the cost of the output spiking to an extremely large value. This is one of the things that must be kept in mind when selecting the gain values.
This project (and course) was extremely interesting and affirmed my interest in control systems. While I understand that classical control and PID controllers are extremely common in industry, I am excited to continue to learn more about control in my future endeavours.